สั่งไข่เจียว 2 ฟอง 4 อย่าง 35 บาทกินทุกวันไม่ซ้ำแบบกัน ได้นานที่สุดกี่วัน
นายซาก้อนอยากกินไข่เจียว 2 ฟอง 4 อย่างเป็นข้าวเย็นทุกวัน แต่ถ้าเป็นไปได้เขาอยากสั่งเครื่องให้ไม่ซ้ำแบบกันให้นานที่สุดเท่าที่จะทำได้


นายซาก้อนอยากกินไข่เจียว 2 ฟอง 4 อย่างเป็นข้าวเย็นทุกวัน แต่ถ้าเป็นไปได้เขาอยากสั่งเครื่องให้ไม่ซ้ำแบบกันให้นานที่สุดเท่าที่จะทำได้
มีเครื่อง 17 อย่าง จงหาจำนวนวันมากที่สุดที่เขาสามารถสั่งไข่เจียวไม่ซ้ำแบบกันได้ กำหนดให้ต้องสั่ง 4 อย่างและสามารถเลือกเครื่องอย่างเดียวกันซ้ำกันได้
แถวนี้ไม่มีร้านข้าวไข่เจียวมาเปิดนานประมาณ 2-3 ปีแล้ว เพื่อเป็นการฉลองเรามาลองคำนวณกันซักหน่อย
Derive สูตร combination with repetition
มีสูตรสำเร็จด้วยแต่เพื่อให้จำได้เราจะ derive มาเข้าสูตร combination ปกติกันให้ได้
วิธีคิดอาจจะคิดว่าเป็นกระดานที่บอกว่าจะเอาอันไหนให้เอาสติกเกอร์มาแปะระหว่างเส้นคั่น แต่มีสติกเกอร์ให้จำกัดจำนวน
เช่นถ้ามีเครื่อง 3 อย่างเลือกได้ 5 ครั้ง ก็เหมือนมีสติกเกอร์ 5 อันกับที่คั่น 2 แท่ง
xx | x | xx เลือกเครื่องใส่ไข่คือ 2–1–2
| xxxx | xเลือก 0–4–1 อาจจะไม่ชอบอย่างแรกเลยไม่เอา
| | xxxxxแบบนี้เลือกแต่อย่างที่สาม อาจจะชอบแค่อย่างสุดท้าย
เปลี่ยนให้เป็น combination ปกติ
ที่ยกตัวอย่างมาแค่ 3 pattern คำถามก็เลยเปลี่ยนได้เป็นว่า มีเรียง 2 แท่งกับ 5 x งี้ได้กี่แบบทั้งหมด
ก็คือ C(7,5) เพราะถ้าคิดว่ามีสิ่ง 7 สิ่งที่ความหมายต่างกัน แล้วมี 5 อันในนั้นที่จะโดน x (ไม่สนลำดับ) ถ้า 3 อย่าง 5 ครั้งได้ C(7,5)
ก็หมายความว่าสูตรคือ C(อย่าง+ครั้ง-1, ครั้ง)
อย่าลืมว่าสูตรของ combination C(n,k) คือ
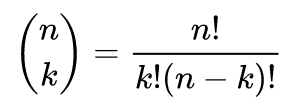
ใช้สูตรคิดคำตอบ
เครื่อง 17 อย่างเลือก 4 ครั้ง C(17+4–1, 4) = C(20,4) = 20!/4!(20–4)! = 20*19*18*…*6*5 / 16*15*…*2*1 = 4845 แบบ เท่ากับกินไข่เจียวทุกวันได้ประมาณ 4845 / 365 = 13.27 ปี
ปล.ไม่ได้จำสูตรได้ กินไข่เจียวแล้วสงสัยเลยไป google หาสูตรมา 555